数据结构Tree

tree树是一种常见的数据结构，我这里我们只讨论BST(二叉搜索树)，AVL(平衡树),RBT(红黑树)。 BST与AVL是学习红黑树的基础，这里推荐学习七月子空

的讲解，很详细。

二叉搜索树

左子节点值总是小于当前节点，右子节点值总是大于当前节点，所以寻找节点时根据寻找节点的值大于还是小于当前节点

一次递归下去直到null值 所以整个查找过程就是从根节点开始一直向下的一条路径，若假设树的高度是h，那么查找过程的时间复杂度就是O(h)。

AVL平衡树，相对于BST的特点就是 左右两边树的高度是平衡的，也就是任意子树高度不会高过另一子树1 ,这样的优点就是大大增加了查询的效率，例如BST遇到这样的树

左为平衡树 右为非平衡树查询效率就会相对低，那AVL树是如何保证树总是平衡呢，这里就到了树旋转的操作，分为左旋和右旋，语言表达能力有限，可以自行百度左旋右旋的操作 当有节点插入或者删除时AVL树就会有一个平衡适应的操作通过不断旋转，保持树的平衡因子不超过1，树的平衡因子也就是左右子树高度差值。

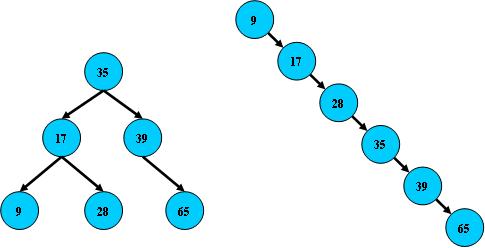
RBT红黑树，一种高级数据结构，很多linux源码中使用，以及很多语言都有相关的实现 RBT 树是相对平衡的 查询效率高 插入删除高于AVL树 每次插入新节点必为红色 因为如果为黑色无形的打破了 从根节点到子节点黑色节点个数相同的规则 黑高 若经过调整新节点为根节点最后会将根节点染黑 RBT 插入调整旋转 最多旋转2次 插入调整情况(fixAfterInsertion) 1.插入X为根节点 直接将X由红染黑 简称rootover 2.父节点P为黑色，BlackParentOver 简称bpOver 所以只需要考虑父节点为P为红色的情况，由于相邻两个节点不能为红色所以爷爷一定为黑色 分为三种情况

case1.Y 为红色,X可以为左孩子或者右孩子: P,Y染黑 G染红 X回溯至G

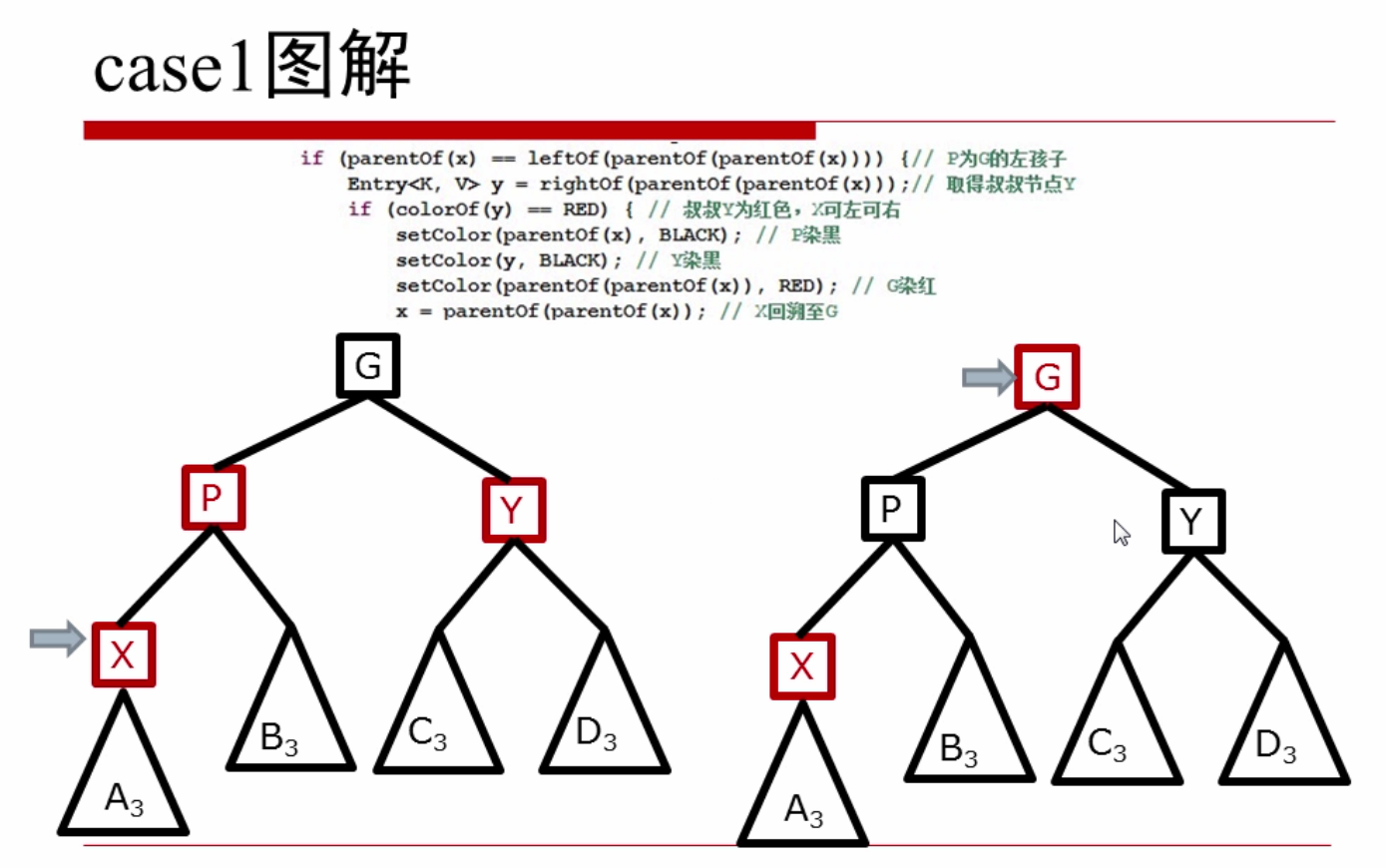
case2. Y为黑色 X为右孩子: 左旋P X指向P 转化为case3

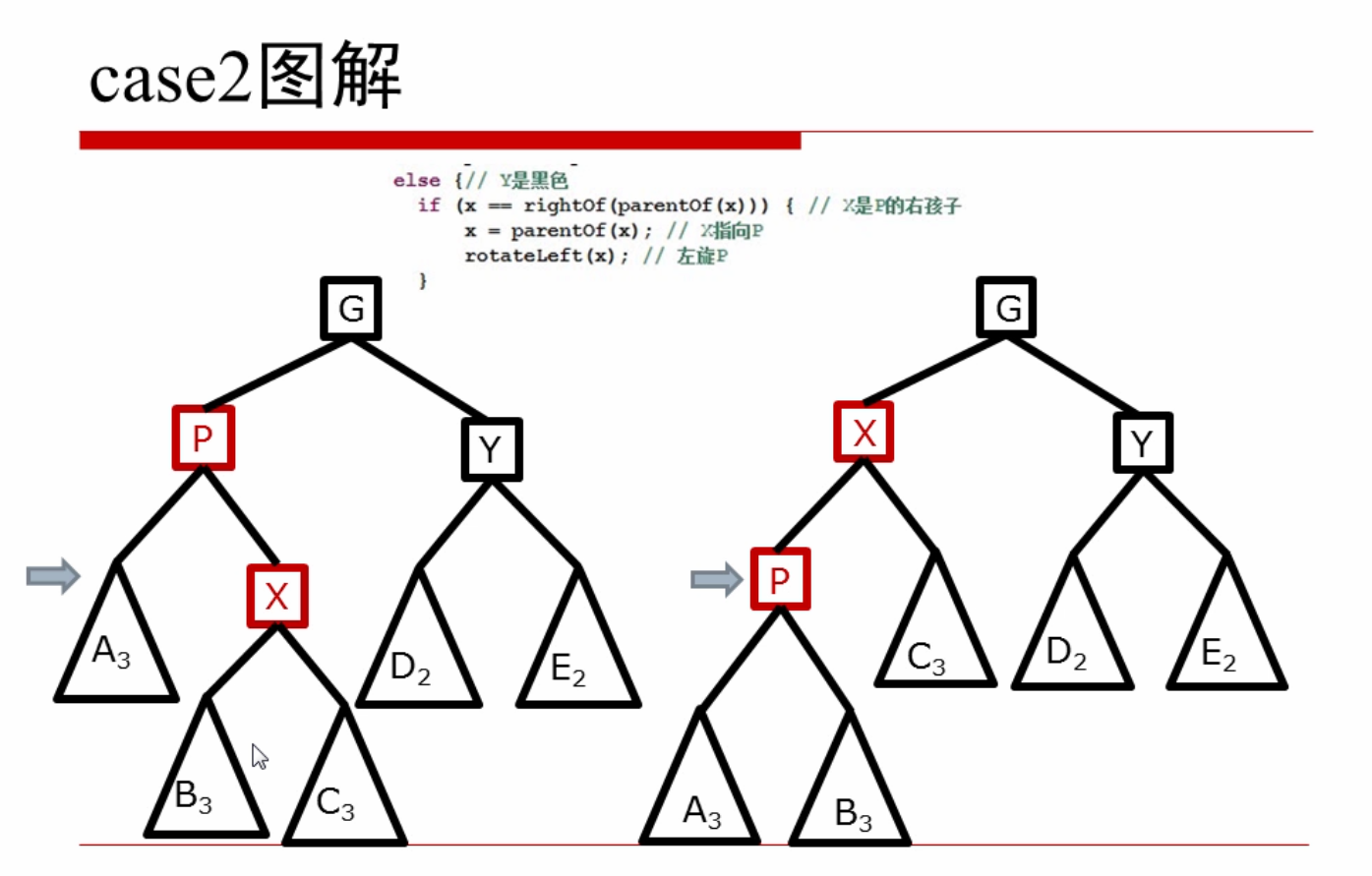
case3.Y为黑色，X为左孩子：P染黑 G染红 右旋G 结束

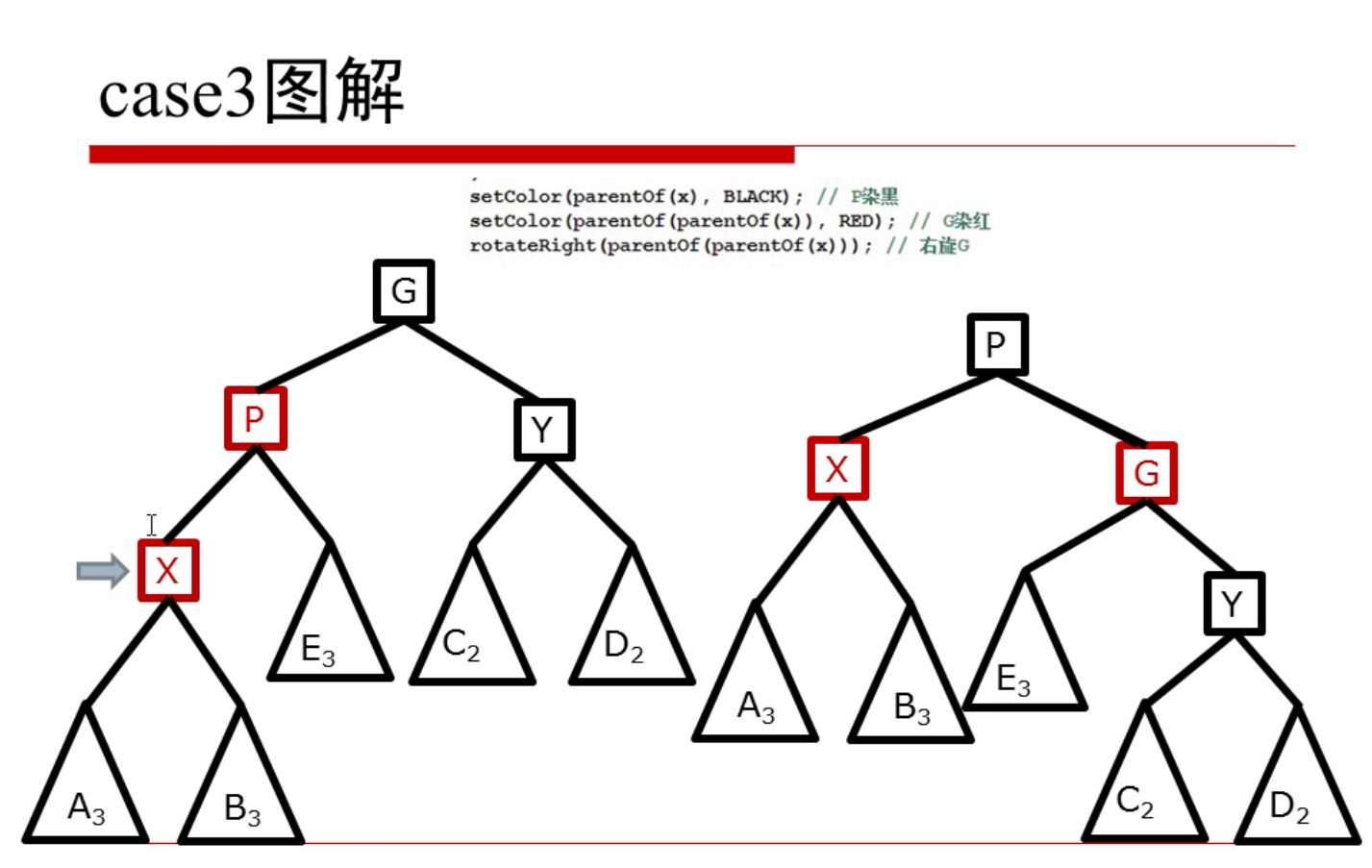
AVL与RBT 插入调整对比

RBT 删除调整

删除调整(fixAfterDeletion) case1.兄弟节点S为红色 兄弟节点染黑 父节点染红 左旋P case2.兄弟节点S为黑色 黑LN，黑RN ； S染红 X回溯P case3.兄弟节点S为黑色 红LN 黑RN ； LN染黑 S染红 ，右旋S case4.黑S兄弟节点 LN随意，红RN ； S变P颜色 P和RN染黑，左旋P