插入排序

思路

遍历数组将每个元素与前面元素一一对比 如果小于就换位 最好情况O(n) 最坏情况O(n²) 建议数组长度较小时使用

 /**
     * 插入排序
     *
     * @param arr
     */
    public static void insertionSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            int j = i;
            while (j > 0 && arr[j] < arr[j - 1]) {
                swap(arr,j,j-1);
                j--;
            }
        }
    }

快速排序

思路

取一基准值 将小于该基准值放在数组左侧 大于基准值放于右侧 递归左右区间

传统单轴快排缺陷 对于有序集合排序很慢属于不稳定排序算法 最坏情况O(n²) 最好情况O(n) 平均情况log₂n

优化方法

快速排序算法主要取决于基准值选取

1.simple以数组首元素或者尾元素为基准不稳定 对于有序数据会大大延长排序速度 对于相对打散集合效果相对较好

2.rand 随机选取数组内元素为基准值 绝对安全 但是当数据量比较大时 频繁的调用rand产生随机数 浪费性能 适得其反 适用于小数据量集

3.mid 三值取中法 相对稳定 排序表现良好 建议采取

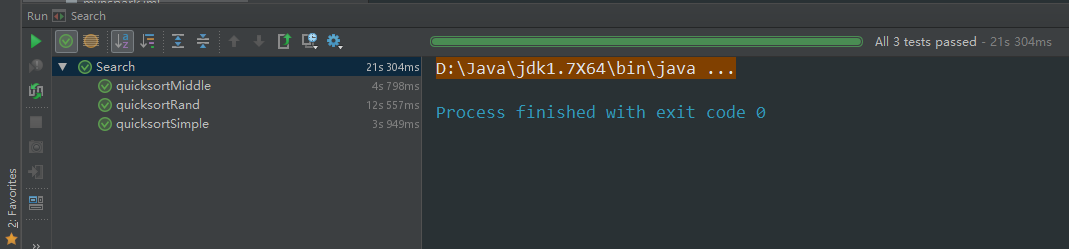
1000以内 500w 密集形数据 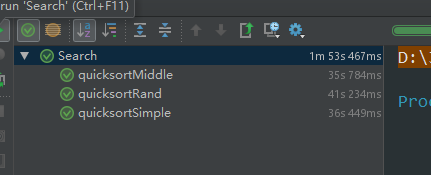1000000以内 500w 松散形数据

归并排序

思路

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。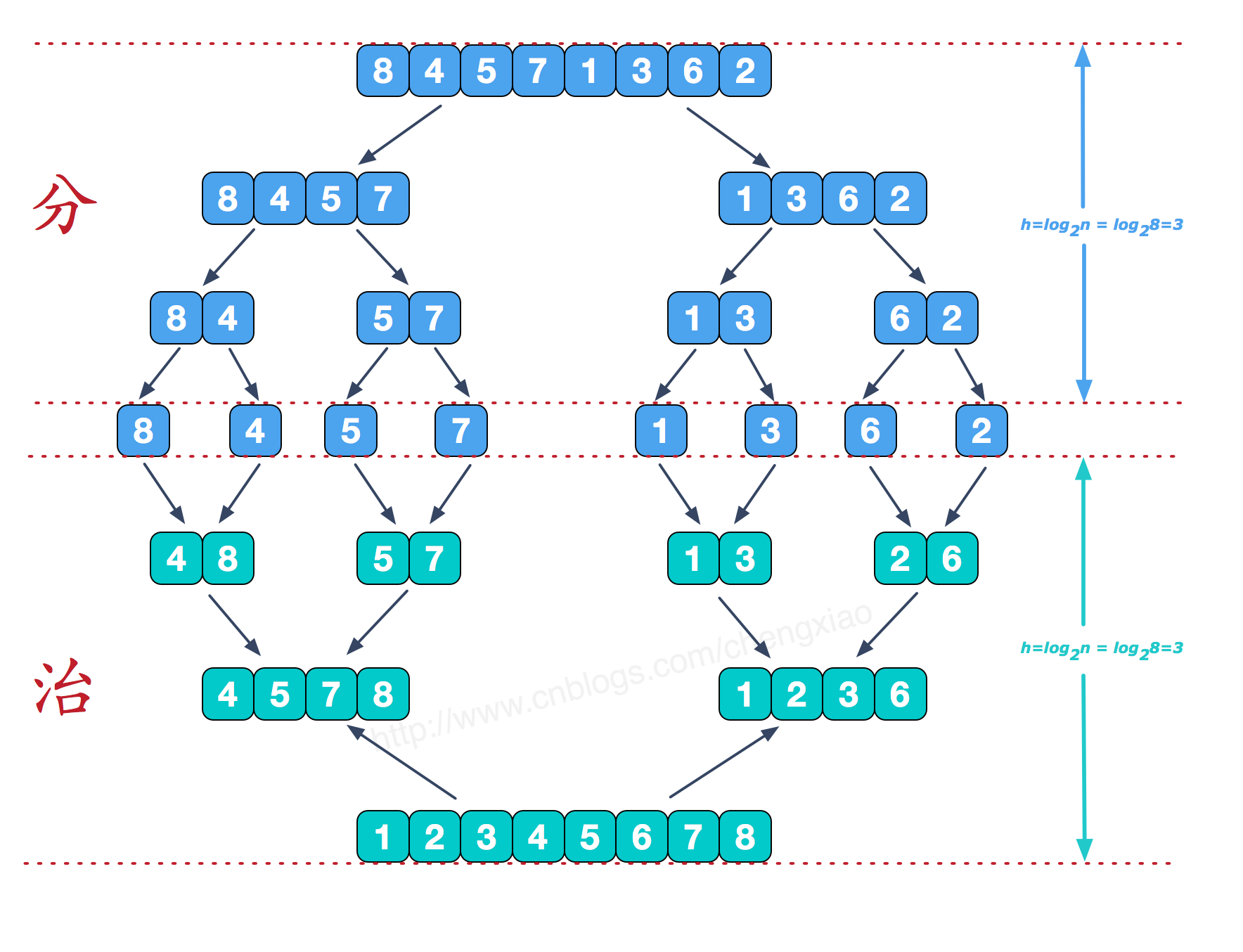

package sortdemo;

import java.util.Arrays;

/**
 * Created by chengxiao on 2016/12/8.
 */
public class MergeSort {
    public static void main(String []args){
        int []arr = {9,8,7,6,5,4,3,2,1};
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }
    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        sort(arr,0,arr.length-1,temp);
    }
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left<right){
            int mid = (left+right)/2;
            sort(arr,left,mid,temp);//左边归并排序，使得左子序列有序
            sort(arr,mid+1,right,temp);//右边归并排序，使得右子序列有序
            merge(arr,left,mid,right,temp);//将两个有序子数组合并操作
        }
    }
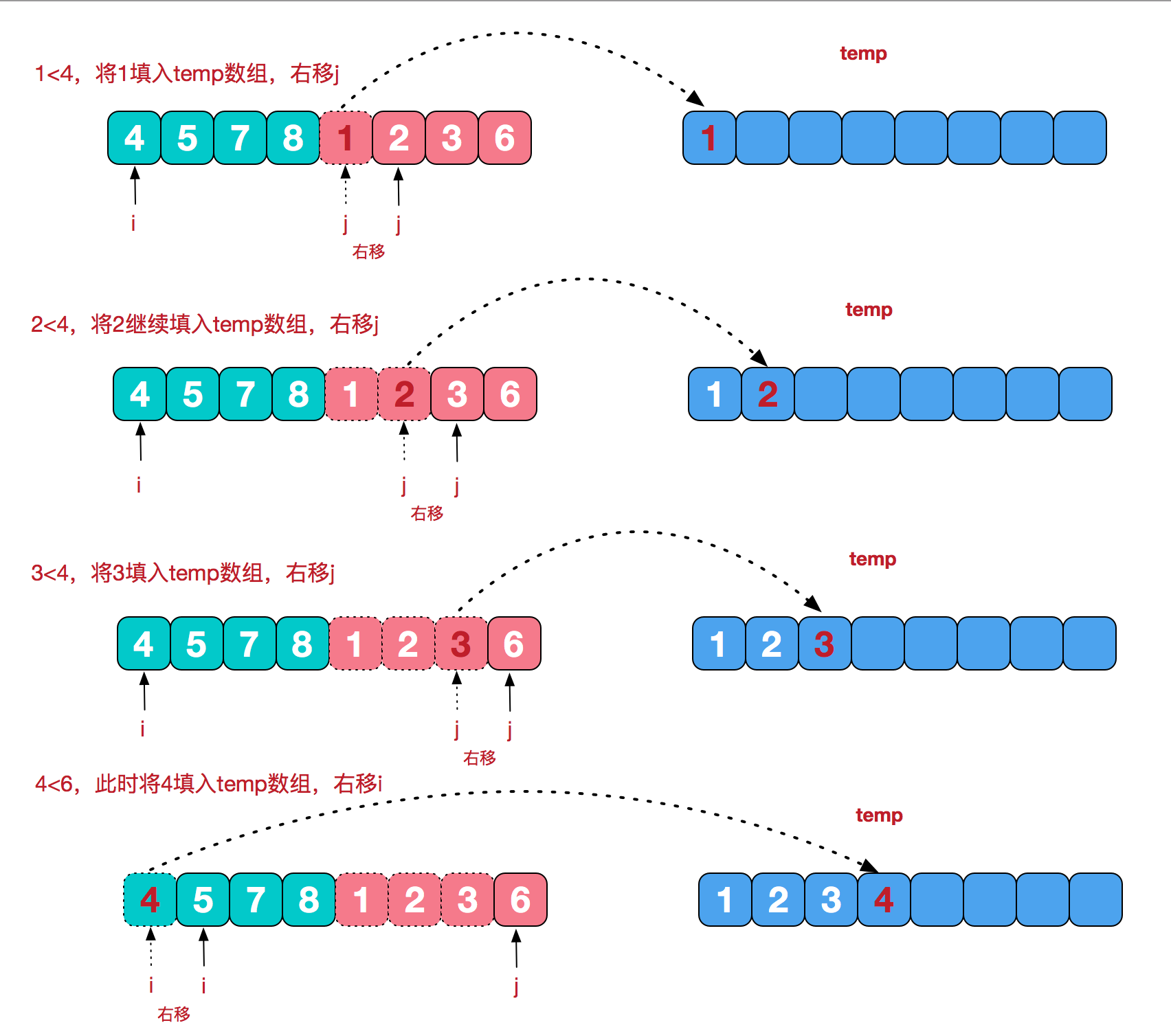
    private static void merge(int[] arr,int left,int mid,int right,int[] temp){
        int i = left;//左序列指针
        int j = mid+1;//右序列指针
        int t = 0;//临时数组指针
        while (i<=mid && j<=right){
            if(arr[i]<=arr[j]){
                temp[t++] = arr[i++];
            }else {
                temp[t++] = arr[j++];
            }
        }
        while(i<=mid){//将左边剩余元素填充进temp中
            temp[t++] = arr[i++];
        }
        while(j<=right){//将右序列剩余元素填充进temp中
            temp[t++] = arr[j++];
        }
        t = 0;
        //将temp中的元素全部拷贝到原数组中
        while(left <= right){
            arr[left++] = temp[t++];
        }
    }
}

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。

从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

从JDK7开始采用这种双Pivot的快速排序算法,首先会根据数组的长度选择对应的排序算法 1.需要排序的数组为a,判断数组的长度是否大于286，大于使用归并排序（merge sort），否则执行2。 2.判断数组长度是否小于47，小于则采用插入排序，否则执行3。 3.双轴快排 采用近似算法计算数组长度的1/7

int seventh = (length >> 3) + (length >> 6) + 1;

取出5个点

int e3 = (left + right) >>> 1; // 中位数
int e2 = e3 - seventh;
int e1 = e2 - seventh;
int e4 = e3 + seventh;
int e5 = e4 + seventh;

5.将这5个元素进行插入排序

6.选取a[e2],a[e4]分别作为pivot1，pivot2。由于步骤5进行了排序，所以必有pivot1 < pivot2。

7.接下来定义3个指针，分别是less,k,great。先说一下最终结果，less和great将数组分为3个部分，分别是小于less的，大于less小于great的元素和大于great的元素。 如何达到这个结果呢，初始时，less和great分别指向数组起始的元素和结束的元素。此时，所有的元素在less和great之间，即待处理的元素。随着程序的进行，小于less的元素逐步移动到less左边，大于great的元素移动到great右边。 另外有一个指针k表示处理到哪个元素了，初始值为less，结束值为great（这里的great是会动态改变的，但是大于great的元素一定是处理过的）

8.将a[k]分别与pivot1，pivot2比较。如果小于pivot1，则将a[k]与a[less]对调，同时k++。如果大于pivot2，则执行9；否则执行10。 9.将a[great]分别与pivot1，pivot2比较。如果a[great]大于pivot2，则递减great，直到大于pivot2的条件不满足或者k==great。如果a[great]小于pivot1，则将a[great]换到小于less的区域。如果a[great]大于pivot1，则说明位于中间区域，将a[great]与a[k]对调。great–。 10.k++，如果k>great,说明处理完成，则执行11，否则继续执行8； 11.由于前面的操作，还未将pivot1，pivot2这2个元素放对位置，所以还需要将a[less - 1]移动到队头，pivot1移动到（less - 1）的位置，将a[great +1]移动到队尾，pivot2移动到（great +1）的位置。 12.至此，已经达到步骤7描述的最终结果，将数组分为了3个区域。对较小的区域和较大的区域递归执行步骤2。判断中间的区域是否过大，如果是，则执行13，否则递归执行步骤2。 13.将等于pivot1或者pivot2的元素移动到两边，然后递归执行步骤2。